The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.

• Home
• The Book by Chapters
• About the Book
  • Copyright and permissible use
  • What is DSP?
  • 8 good reasons for learning DSP
  • Comments by reviewers
  • Errata
  • Free Software and Teaching Aids
  • Differences Between Editions
• Steven W. Smith
• Blog
• Contact

The Discrete Time Fourier Transform (DTFT) is the member of the Fourier transform family that operates on aperiodic, discrete signals. The best way to understand the DTFT is how it relates to the DFT. To start, imagine that you acquire an N sample signal, and want to find its frequency spectrum. By using the DFT, the signal can be decomposed into sine and cosine waves, with frequencies equally spaced between zero and one-half of the sampling rate. As discussed in the last chapter, padding the time domain signal with zeros makes the period of the time domain longer, as well as making the spacing between samples in the frequency domain narrower. As N approaches infinity, the time domain becomes aperiodic, and the frequency domain becomes a continuous signal. This is the DTFT, the Fourier transform that relates an aperiodic, discrete signal, with a periodic, continuous frequency spectrum.

The mathematics of the DTFT can be understood by starting with the synthesis and analysis equations for the DFT (Eqs. 8-2, 8-3 and 8-4), and taking N to infinity:

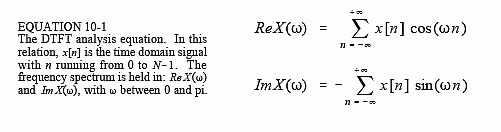
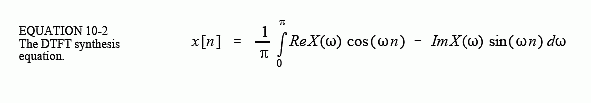
There are many subtle details in these relations. First, the time domain signal, x[n], is still discrete, and therefore is represented by brackets. In comparison, the frequency domain signals, ReX(ω) & ImX(ω), are continuous, and are thus written with parentheses. Since the frequency domain is continuous, the synthesis equation must be written as an integral, rather than a summation.

As discussed in Chapter 8, frequency is represented in the DFT's frequency domain by one of three variables: k, an index that runs from 0 to N/2; f, the fraction of the sampling rate, running from 0 to 0.5; or ω, the fraction of the sampling rate expressed as a natural frequency, running from 0 to π. The spectrum of the DTFT is continuous, so either f or ω can be used. The common choice is ω, because it makes the equations shorter by eliminating the always present factor of 2π. Remember, when ω is used, the frequency spectrum extends from 0 to π, which corresponds to DC to one-half of the sampling rate. To make things even more complicated, many authors use Ω (an upper case omega) to represent this frequency in the DTFT, rather than ω (a lower case omega).

When calculating the inverse DFT, samples 0 and N/2 must be divided by two (Eq. 8-3) before the synthesis can be carried out (Eq. 8-2). This is not necessary with the DTFT. As you recall, this action in the DFT is related to the frequency spectrum being defined as a spectral density, i.e., amplitude per unit of bandwidth. When the spectrum becomes continuous, the special treatment of the end points disappear. However, there is still a normalization factor that must be included, the 2/N in the DFT (Eq. 8-3) becomes 1/π in the DTFT (Eq. 10-2). Some authors place these terms in front of the synthesis equation, while others place them in front of the analysis equation. Suppose you start with some time domain signal. After taking the Fourier transform, and then the Inverse Fourier transform, you want to end up with what you started. That is, the 1/π term (or the 2/N term) must be encountered somewhere along the way, either in the forward or in the inverse transform. Some authors even split the term between the two transforms by placing 1/√π in front of both.

Since the DTFT involves infinite summations and integrals, it cannot be calculated with a digital computer. Its main use is in theoretical problems as an alternative to the DFT. For instance, suppose you want to find the frequency response of a system from its impulse response. If the impulse response is known as an array of numbers, such as might be obtained from an experimental measurement or computer simulation, a DFT program is run on a computer. This provides the frequency spectrum as another array of numbers, equally spaced between 0 and 0.5 of the sampling rate.

In other cases, the impulse response might be know as an equation, such as a sinc function or an exponentially decaying sinusoid. The DTFT is used here to mathematically calculate the frequency domain as another equation, specifying the entire continuous curve between 0 and 0.5. While the DFT could also be used for this calculation, it would only provide an equation for samples of the frequency response, not the entire curve.