The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.

• Home
• The Book by Chapters
• About the Book
  • Copyright and permissible use
  • What is DSP?
  • 8 good reasons for learning DSP
  • Comments by reviewers
  • Errata
  • Free Software and Teaching Aids
  • Differences Between Editions
• Steven W. Smith
• Blog
• Contact

Unwanted convolution is an inherent problem in transferring analog information. For instance, all of the following can be modeled as a convolution: image blurring in a shaky camera, echoes in long distance telephone calls, the finite bandwidth of analog sensors and electronics, etc. Deconvolution is the process of filtering a signal to compensate for an undesired convolution. The goal of deconvolution is to recreate the signal as it existed before the convolution took place. This usually requires the characteristics of the convolution (i.e., the impulse or frequency response) to be known. This can be distinguished from blind deconvolution, where the characteristics of the parasitic convolution are not known. Blind deconvolution is a much more difficult problem that has no general solution, and the approach must be tailored to the particular application.

Deconvolution is nearly impossible to understand in the time domain, but quite straightforward in the frequency domain. Each sinusoid that composes the original signal can be changed in amplitude and/or phase as it passes through the undesired convolution. To extract the original signal, the deconvolution filter must undo these amplitude and phase changes. For

example, if the convolution changes a sinusoid's amplitude by 0.5 with a 30 degree phase shift, the deconvolution filter must amplify the sinusoid by 2.0 with a -30 degree phase change.

The example we will use to illustrate deconvolution is a gamma ray detector. As illustrated in Fig. 17-3, this device is composed of two parts, a scintillator and a light detector. A scintillator is a special type of transparent material, such as sodium iodide or bismuth germanate. These compounds change the energy in each gamma ray into a brief burst of visible light. This light

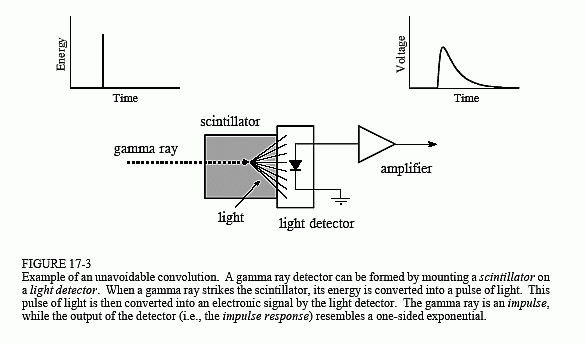
is then converted into an electronic signal by a light detector, such as a photodiode or photomultiplier tube. Each pulse produced by the detector resembles a one-sided exponential, with some rounding of the corners. This shape is determined by the characteristics of the scintillator used. When a gamma ray deposits its energy into the scintillator, nearby atoms are excited to a higher energy level. These atoms randomly deexcite, each producing a single photon of visible light. The net result is a light pulse whose amplitude decays over a few hundred nanoseconds (for sodium iodide). Since the arrival of each gamma ray is an impulse, the output pulse from the detector (i.e., the one-sided exponential) is the impulse response of the system.

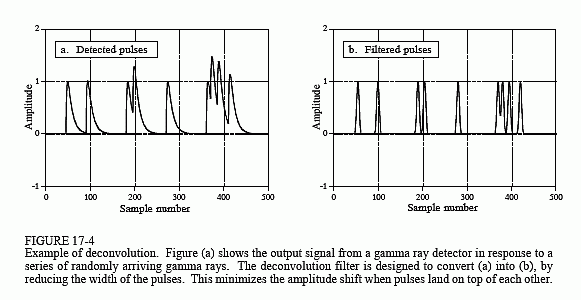
Figure 17-4a shows pulses generated by the detector in response to randomly arriving gamma rays. The information we would like to extract from this output signal is the amplitude of each pulse, which is proportional to the energy of the gamma ray that generated it. This is useful information because the energy can tell interesting things about where the gamma ray has been. For example, it may provide medical information on a patient, tell the age of a distant galaxy, detect a bomb in airline luggage, etc.

Everything would be fine if only an occasional gamma ray were detected, but this is usually not the case. As shown in (a), two or more pulses may overlap, shifting the measured amplitude. One answer to this problem is to deconvolve the detector's output signal, making the pulses narrower so that less pile-up occurs. Ideally, we would like each pulse to resemble the original impulse. As you may suspect, this isn't possible and we must settle for a pulse that is finite in length, but significantly shorter than the detected pulse. This goal is illustrated in Fig. 17-4b.

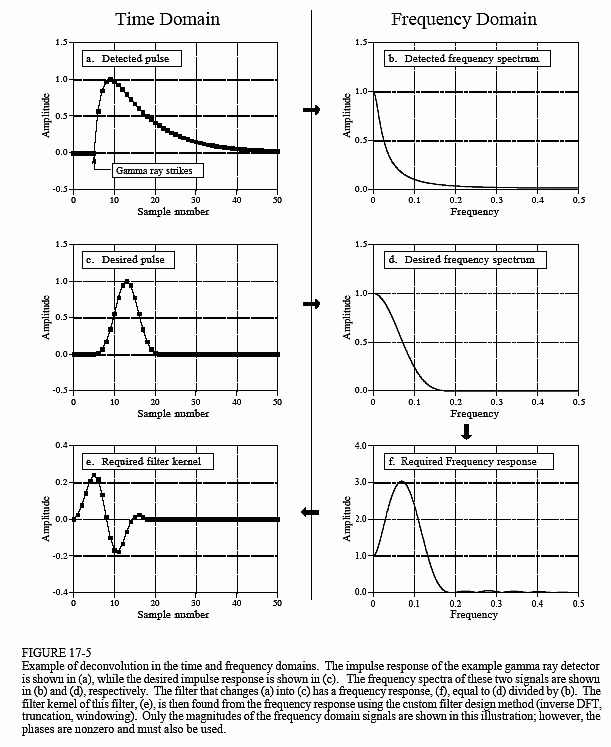
Even though the detector signal has its information encoded in the time domain, much of our analysis must be done in the frequency domain, where the problem is easier to understand. Figure 17-5a is the signal produced by the detector (something we know). Figure (c) is the signal we wish to have (also something we know). This desired pulse was arbitrarily selected to be the same shape as a Blackman window, with a length about one-third that of the original pulse. Our goal is to find a filter kernel, (e), that when convolved with the signal in (a), produces the signal in (c). In equation form: if a * e = c, and given a and c, find e.

If these signals were combined by addition or multiplication instead of convolution, the solution would be easy: subtraction is used to "de-add" and division is used to "de-multiply". Convolution is different; there is not a simple inverse operation that can be called "deconvolution." Convolution is too messy to be undone by directly manipulating the time domain signals.

Fortunately, this problem is simpler in the frequency domain. Remember, convolution in one domain corresponds with multiplication in the other domain. Again referring to the signals in Fig. 17-5: if b × f = d, and given b and d, find f. This is an easy problem to solve: the frequency response of the filter, (f), is the frequency spectrum of the desired pulse, (d), divided by the frequency spectrum of the detected pulse, (b). Since the detected pulse is asymmetrical, it will have a nonzero phase. This means that a complex division must be used (that is, a magnitude & phase divided by another magnitude & phase). In case you have forgotten, Chapter 9 defines how to perform a complex division of one spectrum by another. The required filter kernel, (e), is then found from the frequency response by the custom filter method (IDFT, shift, truncate, & multiply by a window).

There are limits to the improvement that deconvolution can provide. In other words, if you get greedy, things will fall apart. Getting greedy in this example means trying to make the desired pulse excessively narrow. Let's look at what happens. If the desired pulse is made narrower, its frequency spectrum must contain more high frequency components. Since these high frequency components are at a very low amplitude in the detected pulse, the filter must have a very high gain at these frequencies. For instance, (f) shows that some frequencies must be multiplied by a factor of three to achieve the desired pulse in (c). If the desired pulse is made narrower, the gain of the deconvolution filter will be even greater at high frequencies.

The problem is, small errors are very unforgiving in this situation. For instance, if some frequency is amplified by 30, when only 28 is required, the deconvolved signal will probably be a mess. When the deconvolution is pushed to greater levels of performance, the characteristics of the unwanted convolution must be understood with greater accuracy and precision. There are always unknowns in real world applications, caused by such villains as: electronic noise, temperature drift, variation between devices, etc. These unknowns set a limit on how well deconvolution will work.

Even if the unwanted convolution is perfectly understood, there is still a factor that limits the performance of deconvolution: noise. For instance, most unwanted convolutions take the form of a low-pass filter, reducing the amplitude of the high frequency components in the signal. Deconvolution corrects this by amplifying these frequencies. However, if the amplitude of these components falls below the inherent noise of the system, the information contained in these frequencies is lost. No amount of signal processing can retrieve it. It's gone forever. Adios! Goodbye! Sayonara! Trying to reclaim this data will only amplify the noise. As an extreme case, the amplitude of some frequencies may be completely reduced to zero. This not only obliterates the information, it will try to make the deconvolution filter have infinite gain at these frequencies. The solution: design a less aggressive deconvolution filter and/or place limits on how much gain is allow at any of the frequencies.

How far can you go? How greedy is too greedy? This depends totally on the problem you are attacking. If the signal is well behaved and has low noise, a significant improvement can probably be made (think a factor of 5-10). If the signal changes over time, isn't especially well understood, or is noisy, you won't do nearly as well (think a factor of 1-2). Successful deconvolution involves a great deal of testing. If it works at some level, try going farther; you will know when it falls apart. No amount of theoretical work will allow you to bypass this iterative process.

Deconvolution can also be applied to frequency domain encoded signals. A classic example is the restoration of old recordings of the famous opera singer, Enrico Caruso (1873-1921). These recordings were made with very primitive equipment by modern standards. The most significant problem is the resonances of the long tubular recording horn used to gather the sound. Whenever the singer happens to hit one of these resonance frequencies, the loudness of the recording abruptly increases. Digital deconvolution has improved the subjective quality of these recordings by

reducing the loud spots in the music. We will only describe the general method; for a detailed description, see the original paper: T. Stockham, T. Cannon, and R. Ingebretsen, "Blind Deconvolution Through Digital Signal Processing", Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.

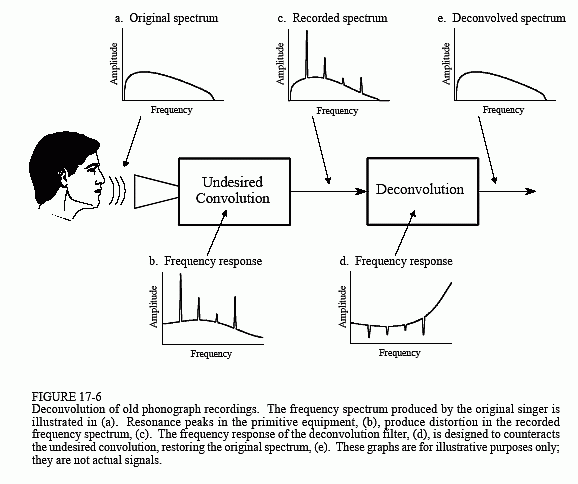
Figure 17-6 shows the general approach. The frequency spectrum of the original audio signal is illustrated in (a). Figure (b) shows the frequency response of the recording equipment, a relatively smooth curve except for several sharp resonance peaks. The spectrum of the recorded signal, shown in (c), is equal to the true spectrum, (a), multiplied by the uneven frequency response, (b). The goal of the deconvolution is to counteract the undesired convolution. In other words, the frequency response of the deconvolution filter, (d), must be the inverse of (b). That is, each peak in (b) is cancelled by a corresponding dip in (d). If this filter were perfectly designed, the resulting signal would have a spectrum, (e), identical to that of the original.

Here's the catch: the original recording equipment has long been discarded, and its frequency response, (b), is a mystery. In other words, this is a blind deconvolution problem; given only (c), how can we determine (d)?

Blind deconvolution problems are usually attacked by making an estimate or assumption about the unknown parameters. To deal with this example, the average spectrum of the original music is assumed to match the average spectrum of the same music performed by a present day singer using modern equipment. The average spectrum is found by the techniques of Chapter 9: break the signal into a large number of segments, take the DFT of each segment, convert into polar form, and then average the magnitudes together. In the simplest case, the unknown frequency response is taken as the average spectrum of the old recording, divided by the average spectrum of the modern recording. (The method used by Stockham et al. is based on a more sophisticated technique called homomorphic processing, providing a better estimate of the characteristics of the recording system).