The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.

• Home
• The Book by Chapters
• About the Book
  • Copyright and permissible use
  • What is DSP?
  • 8 good reasons for learning DSP
  • Comments by reviewers
  • Errata
  • Free Software and Teaching Aids
  • Differences Between Editions
• Steven W. Smith
• Blog
• Contact

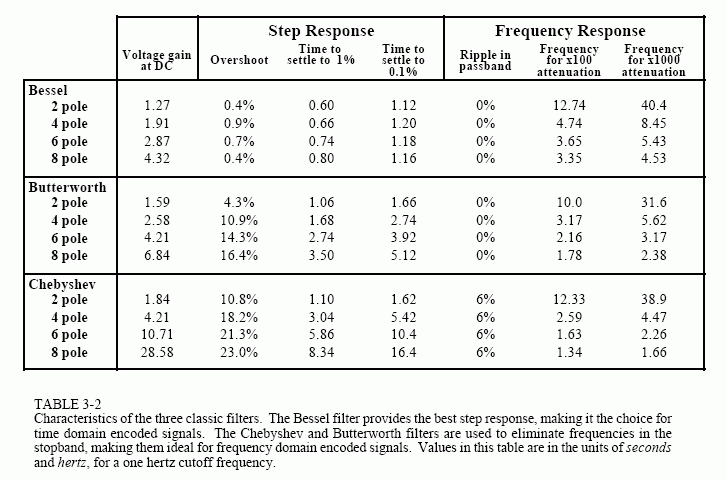
Table 3-2 summarizes the characteristics of these three filters, showing how each optimizes a particular parameter at the expense of everything else. The Chebyshev optimizes the roll-off, the Butterworth optimizes the passband flatness, and the Bessel optimizes the step response.

The selection of the antialias filter depends almost entirely on one issue: how information is represented in the signals you intend to process. While

there are many ways for information to be encoded in an analog waveform, only two methods are common, time domain encoding, and frequency domain encoding. The difference between these two is critical in DSP, and will be a reoccurring theme throughout this book.

In frequency domain encoding, the information is contained in sinusoidal waves that combine to form the signal. Audio signals are an excellent example of this. When a person hears speech or music, the perceived sound depends on the frequencies present, and not on the particular shape of the waveform. This can be shown by passing an audio signal through a circuit that changes the phase of the various sinusoids, but retains their frequency and amplitude. The resulting signal looks completely different on an oscilloscope, but sounds identical. The pertinent information has been left intact, even though the waveform has been significantly altered. Since aliasing misplaces and overlaps frequency components, it directly destroys information encoded in the frequency domain. Consequently, digitization of these signals usually involves an antialias filter with a sharp cutoff, such as a Chebyshev, Elliptic, or Butterworth. What about the nasty step response of these filters? It doesn't matter; the encoded information isn't affected by this type of distortion.

In contrast, time domain encoding uses the shape of the waveform to store information. For example, physicians can monitor the electrical activity of a person's heart by attaching electrodes to their chest and arms (an electrocardiogram or EKG). The shape of the EKG waveform provides the information being sought, such as when the various chambers contract during a heartbeat. Images are another example of this type of signal. Rather than a waveform that varies over time, images encode information in the shape of a waveform that varies over distance. Pictures are formed from regions of brightness and color, and how they relate to other regions of brightness and color. You don't look at the Mona Lisa and say, "My, what an interesting collection of sinusoids."

Here's the problem: The sampling theorem is an analysis of what happens in the frequency domain during digitization. This makes it ideal to under-stand the analog-to-digital conversion of signals having their information encoded in the frequency domain. However, the sampling theorem is little help in understanding how time domain encoded signals should be digitized. Let's take a closer look.

Figure 3-15 illustrates the choices for digitizing a time domain encoded signal. Figure (a) is an example analog signal to be digitized. In this case, the information we want to capture is the shape of the rectangular pulses. A short burst of a high frequency sine wave is also included in this example signal. This represents wideband noise, interference, and similar junk that always appears on analog signals. The other figures show how the digitized signal would appear with different antialias filter options: a Chebyshev filter, a Bessel filter, and no filter.

It is important to understand that none of these options will allow the original signal to be reconstructed from the sampled data. This is because the original signal inherently contains frequency components greater than one-half of the sampling rate. Since these frequencies cannot exist in the digitized signal, the reconstructed signal cannot contain them either. These high frequencies result from two sources: (1) noise and interference, which you would like to eliminate, and (2) sharp edges in the waveform, which probably contain information you want to retain.

The Chebyshev filter, shown in (b), attacks the problem by aggressively removing all high frequency components. This results in a filtered analog signal that can be sampled and later perfectly reconstructed. However, the reconstructed analog signal is identical to the filtered signal, not the original signal. Although nothing is lost in sampling, the waveform has been severely distorted by the antialias filter. As shown in (b), the cure is worse than the disease! Don't do it!

The Bessel filter, (c), is designed for just this problem. Its output closely resembles the original waveform, with only a gentle rounding of the edges. By adjusting the filter's cutoff frequency, the smoothness of the edges can be traded for elimination of high frequency components in the signal. Using more poles in the filter allows a better tradeoff between these two parameters. A common guideline is to set the cutoff frequency at about one-quarter of the sampling frequency. This results in about two samples along the rising portion of each edge. Notice that both the Bessel and the Chebyshev filter have removed the burst of high frequency noise present in the original signal.

The last choice is to use no antialias filter at all, as is shown in (d). This has the strong advantage that the value of each sample is identical to the value of the original analog signal. In other words, it has perfect edge sharpness; a change in the original signal is immediately mirrored in the digital data. The disadvantage is that aliasing can distort the signal. This takes two different forms. First, high frequency interference and noise, such as the example sinusoidal burst, will turn into meaningless samples, as shown in (d). That is, any high frequency noise present in the analog signal will appear as aliased noise in the digital signal. In a more general sense, this is not a problem of the sampling, but a problem of the upstream analog electronics. It is not the ADC's purpose to reduce noise and interference; this is the responsibility of the analog electronics before the digitization takes place. It may turn out that a Bessel filter should be placed before the digitizer to control this problem. However, this means the filter should be viewed as part of the analog processing, not something that is being done for the sake of the digitizer.

The second manifestation of aliasing is more subtle. When an event occurs in the analog signal (such as an edge), the digital signal in (d) detects the change on the next sample. There is no information in the digital data to indicate what happens between samples. Now, compare using no filter with using a Bessel filter for this problem. For example, imagine drawing straight lines between the samples in (c). The time when this constructed line crosses one-half the amplitude of the step provides a subsample estimate of when the edge occurred in the analog signal. When no filter is used, this subsample information is completely lost. You don't need a fancy theorem to evaluate how this will affect your particular situation, just a good understanding of what you plan to do with the data once is it acquired.